三角比　sin・cos・tan　まとめ

　三角比　サイン　sin、コサイン　cos、タンジェント　tanのまとめ。
　sin・cos・tanは直角三角形の底辺　X、垂線　Y、斜辺　Zの比。

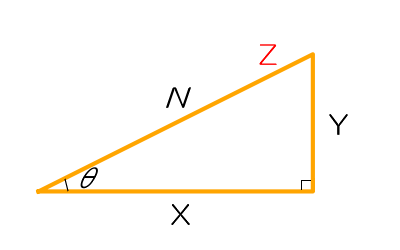
　sinθ ＝垂線　Y ÷ 斜辺　Z
　cosθ ＝底辺　X ÷ 斜辺　Z
　tanθ ＝垂線　Y ÷ 底辺　X

　直角三角形の図を見て
　垂線　Y ＝ Z sinθ
　底辺　X ＝ Z cosθ
　垂線　Y ＝ X tanθ
がパパッと出るようになれば第一関門クリア。

目　次

関係式　その１、その２

　第二関門はいろいろあるsin・cos・tanの関係を知ること。

　その１）tanθ ＝ sinθ／cos θ
　(Y／Z) ÷ (X／Z) ＝ Y／X
　これは簡単。

　その２）sin²θ ＋ cos²θ ＝ 1
　Y² + X² = Z²となる。
　これは三平方の定理（ピタゴラスの定理）の別表現に他ならない。

　こみいった計算式の中にsin² ＋ cos²を見つけて１に変換した後のささやかな安堵感は、我々の頭の片隅に眠っている計算能力を呼び覚ます助けになるかもしれません。

　その３）cos²θ － sin²θ ＝ cos 2θ
　　　　　2θはθの２倍角
　これは？

　前回の放物線軌道の式で、元の高さに落下すなわち飛んだ距離は
　x = (2v₀²sinθcosθ)／g。
　このxは、斜角　θ＝45°のとき、最大すなわち最も遠くへ飛ぶ。

　実際には物体は質点ではなく空気抵抗を受ける。
　野球の場合、ボールには回転もかかって、角度40°以上のホームランは少ない。
　最も遠くへ飛ぶ角度は30°ぐらいとされる。

　で、
　sinθの最大がθ＝90°（＝π/2）で１
　cosθの最大がθ＝0°で１
と知っていても
　sinθcosθの最大は何だろう？となる。１より小さいことは確かだが……。

　y＝sin x・cos xの図を描いてみる。

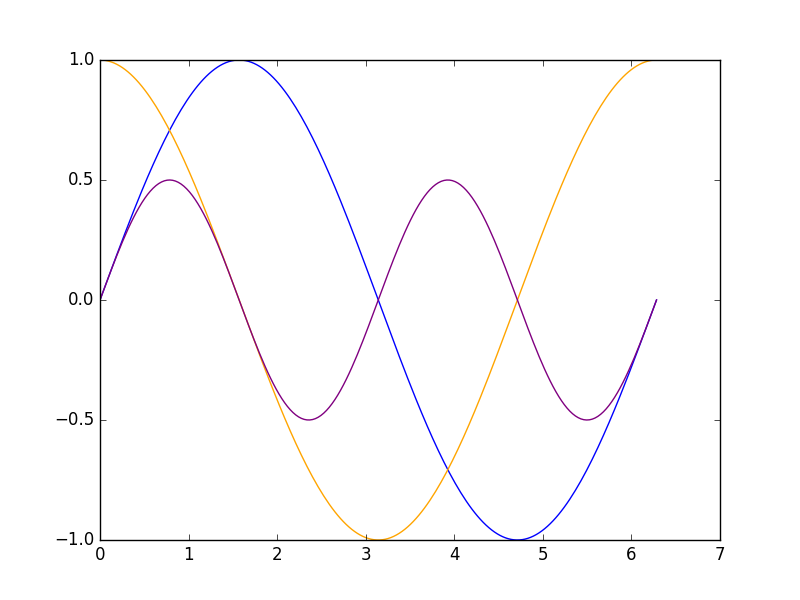
　上図の紫色の曲線がsin x・cos x。
　最大（ピーク）は0.5。
　x＝0.785（＝π/4）つまりθ＝45°のとき最大。

　飛んだ距離　xの最大は、xの式をθで微分して０になる（増減０でピークになる）θを求める。
　dx／dθ ＝ (2v₀²／g)(cosθcosθ－sinθsinθ)
　　※　sinθ微分　⇒　cosθ
　　　　cosθ微分　⇒　－sinθ
　　　　(xy)’ ＝ x’y＋xy’

　ここでcos²θ－sin²θがcos 2θになる。
　俄かには分からない変換だが、
　ひとまずcos 2θ＝0になるθは45°（cos 90＝0なので）。

　青色の曲線がsin、橙色の曲線がcos。
　sin 0＝0、cos 0＝1
　sin 90＝1、cos 90＝0

　関連して
　その３’）sin 2θ ＝ 2sinθcosθ

　sinθcosθの微分は、sin 2θ／2の微分と同じ。cos 2θになる。
　　※　（微分はいつの日かまとめる）

　上のsin 2θ、cos 2θすなわち２倍角の式は
　以下の加法定理から求められる。

　α＝βのとき２倍角の式になる。
　α＝2θ、β＝θとすれば３倍角の式も求められる。
　移項すれば半角の式も。

　この加法定理は図を描いてベクトル使うなどして証明できるが、
　パパパッと導き出せる人は天才。
　拙者省略。
　幸い結果を知っていれば先に進める。

　他にも
　セカント　sec ＝ 1／cos
　コセカント　cosec ＝ 1／sin
　コタンジェント　cot ＝ 1／tan
などなどあるが、
　無理に覚えなくてよいものもある。

　角度の単位は「度　°」の他に「ラジアン　rad」がよく使われる。
　0°～90°～180°～270°～360°と
　0[rad]～π/2[rad]～π[rad]～3/2π[rad]～2π[rad]
が対応している。
　通常、radの表記は省略される。

　扇形の弧長　l＝半径　r ・中心角　θで、
　l＝rのときのθが１[rad]。
　θ＝π[rad]のとき、扇形は半円。l＝πr。
　π＝3.14 [rad] ＝180°
　θ＝2πのとき、円。lは円周。l＝2πr。

　θ°：180° ＝ 1：π
　1[rad] = 180／π ＝ 57.3°

　直角三角形の代表は三角定規でお馴染みの
　45°、45°、90°
　30°、60°、90°

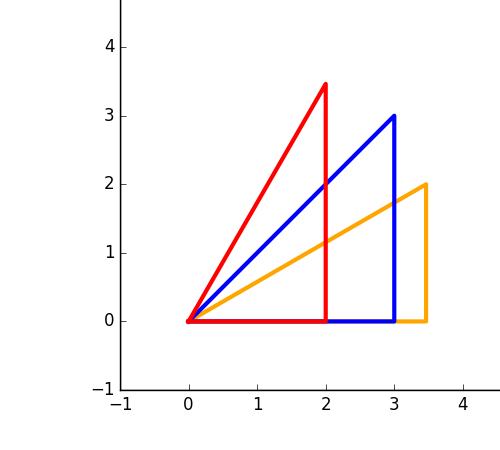
　θ＝45°＝π/4は上図の青色。
　Ｘ：Ｙ：Ｚ＝１：１：√２
　sin 45 ＝ 1/√２、cos 45 ＝ 1/√２、tan 45 = 1
　sin 45・cos 45 ＝ 1/2

　θ＝30°＝π/6は上図の橙色。
　X：Ｙ：Ｚ=√3：１：2
　sin 30 ＝ 1/２、cos 30 ＝ √3/２、tan 30 = 1/√3

　θ＝60°＝π/3は上図の赤色。
　上のＸとＹが入れ代わっただけ。
　sin 60 ＝ √3/２、cos 60 ＝ 1/２、tan 60 = √3

　θ＝18°ならば、
　18°：180° ＝ x：π
　x ＝ 18π／180 ＝ π/10[rad]

　tan 0＝0
　tan 90は１÷０なので無限大　∞

　sinθ、cosθは１を超えることはないが、
　tanθはθ＝45°～90°で１～∞

　y ＝ sin x
　y ＝ cos x
　y ＝ tan x
のx－y関係が三角関数。
　図２の青色の曲線がsin、橙色の曲線がcos。　　