今年は大学入学共通テストが難しくなった、というニュースとともに問題を目にしてしまった。しまった。
※ 昨年から大学入試センター試験が大学入学共通テストに変わった
数学I・数学A 第5問
『△ABCの重心をGとし、線分AG上で点Aとは異なる位置に点Dをとる。直線AGと辺BCの交点をEとする。また、直線BC上で辺BCにはない位置に点Fをとる。直線DFと辺ABの交点をP、直線DFと辺ACの交点をQとする。』
以下、 ■ が埋めていく解答欄。
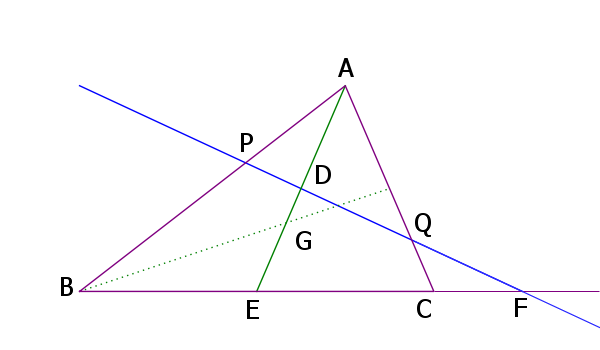
描いてみると下のような図になる。
(1)
『点Dは線分AGの中点であるとする。このとき、△ABCの形状に関係なく、
AD/DE= ■ 』
AD:DG = 1:1なので、点D、P、Qは上の図1よりもう少し上になるが、ひとまず直線と三角形 △に関する問題のよう。
三角形の重心はAG:GE = 2:1。
※ そう決まっている。点Eは辺BCの中点。
AD:DG:GE = 1:1:1で、AD:DE = 1:2。AD/DE = 1/2。
『また、点Fの位置に関係なく、
BP/AP= ■ .CQ/AQ= ■ 』
メネラウスの定理を使う。
ページ下にメモしておいた。
・ △ABCにおいて
AP/PB ・ CQ/QA ・ BF/FC = 1
・ △ADEにおいて
AP/PB ・ AD/DE ・ BF/FE = 1
BP/AP = AD/DE ・ BF/FE = 2BF/EF
CQ/AQ = FC/BF ・ PB/AP = CF/BF ・ 2BF/EF = 2CF/EF
『であるので、つねに
BP/AP + CQ/AQ= ■ 』
BP/AP + CQ/AQ = 2BF/EF + 2CF/EFに
BF = BC + CF、EF = 1/2 BC + CFを代入すると
BP/AP + CQ/AQ = 4(BC + 2CF) / (BC + 2CF) = 4
なお、上のBP/AP、CQ/AQが求められなくても
BP/AP + CQ/AQは、
『点Fの位置に関係なく……つねに』つまり一定の値なので、
求まる。
上の図1において点Fを右へ動かしていくと点Pが下がって点Qが上がって、直線PDQは直線BCFと平行に近づいていく。
点Fが無限遠のとき、△APQが△ABCと(△APDが△ABEと)相似に近づいていくので、
BP/AP ≒ CQ/AQ ≒ DE/AD
AD/DE = 1/2なので
BP/AP + CQ/AQ ≒ 4
(2)
せっかくなので、続きも……。
『AB=9、BC=8、AC=6とし、(1)と同様に、点Dは線分AGの中点であるとする。ここで、4点B、C、Q、Pが同一円周上にあるように点Fをとる。このとき……
AQ= ■ .AP= ■ 』
下のような図になる。上の図1に円を加えただけ。
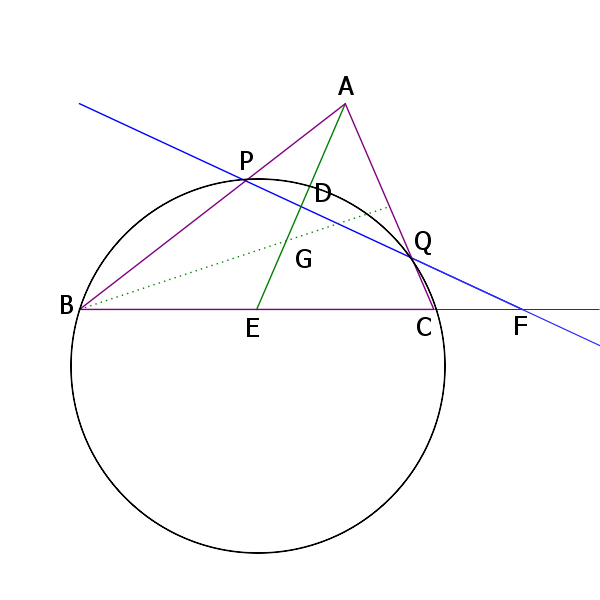
各辺の値が9、8、6でなく、点C、Qもちょっとズレているけどイメージです。
4点が同一円周上にある---
今度は方冪(べき)の定理。
これもページ下にメモしておいたが、
AP ・ AB = AQ ・ AC。
AQ = (AB/AC) ・ AP = 3/2 ・ AP
(1)で導き出したBP/AP + CQ/AQ = 4と
BP = AB - AP、CQ = AC - AQから
(9 - AP)/AP + (12 - 3AP)/3AP = 4
⇒ 27 - 3AP + 12 - 3AP = 12AP
⇒ 39 = 18AP
AP = 13/6、AQ = 13/4
『であり
CF= ■ 』
(1)で導き出したCQ/AQ = 2CF/EFを使うと
2/13 ・ CQ ・ EF = CF
CQ = AC - AQ、EF = 1/2 BC + CFなので、
13CF = 2(6 - 13/4)・(4 + CF)
⇒ 26CF = 44 + 11CF
⇒ 15CF = 44
CF = 44/15
(3)
『△ABCの形状や点Fの位置に関係なく、つねにBP/AP + CQ/AQ = 10となるのは、
AD/DG= ■
のときである』
(1)の最後と同じで、
点Fが無限遠のとき、
BP/AP ≒ CQ/AQ ≒ DE/AD
BP/AP + CQ/AQ = 10になるのはDE/AD = 5のとき。
AE = AD + DEより
AE = 6AD
また、DG = DE - EG、EG = 1/3 AEより
DG = 5AD - 2AD = 3AD
AD/DG = 1/3
制限時間があるので、メネラウスの定理を知っていないと(1)の真ん中、その解答を用いる(2)のCFが求まらない。
上では省いたが、『解答群』からの選択がヒントか……。
知っていなくても(1)の最後と(3)は求まる。
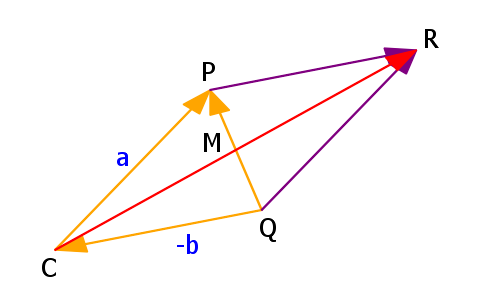
メネラウスの定理
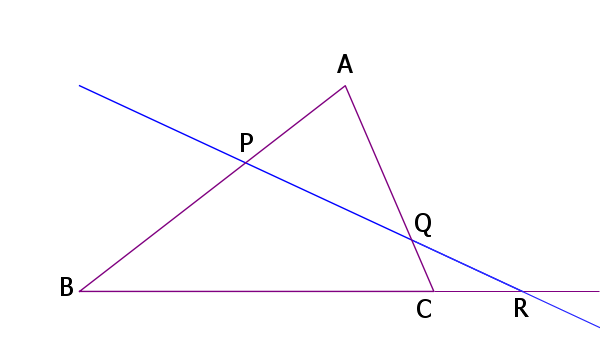
直線PQが直線BCと(点Rで)交わるとき、
AP/PB ・ CQ/QA ・ BR/RC = 1
PとQは辺AB、辺ACの内分点、Rは辺BCの外分点。
△ABCの点A、B、Cから直線PQRに下ろした垂線の足を点S、T、Uとすると
・ △APSと△BPTが相似(∽) ⇒ AP/BP = AS/BT
・ △AQS ∽ △CQU ⇒ AQ/CQ = AS/CU
・ △BRT ∽ △CRU ⇒ BR/CR = BT/CU
AP/BPとCQ/AQとBR/CRを掛けると1になる。
チェバの定理
昔使った参考書を見たらメネラウスの定理の隣に
チェバの定理も載っていた。
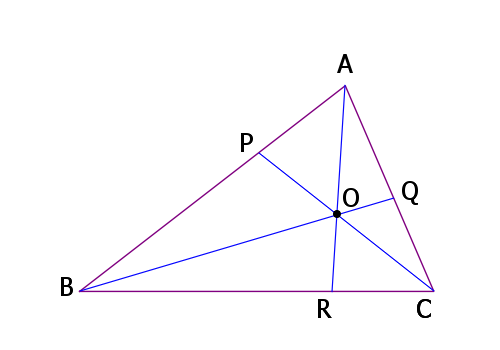
3つの線分AR、BQ、CPが1点で交わるとき、
AP/PB ・ BR/RC ・ CQ/QA = 1
メネラウスの定理を使うと
AP/PB ・ AO/OR ・ BC/CR = 1
AQ/QC ・ AO/OR ・ CB/BR = 1
上2式よりAO/ORを消去すると
AP/PB ・ BC/CR = AQ/QC ・ CB/BR
⇒ AP/PB ・ BR/CR = AQ/QC
全辺内分なのでメネラウスの定理よりも覚えやすい。
方冪(べき)の定理
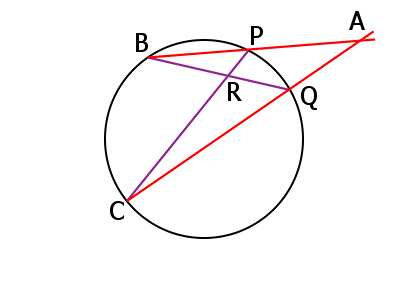
円周上の4点B、C、P、Qと円内で交わる点R、円外で交わる点Aについて、
PR ・ RC = QR ・ RB
AP ・ AB = AQ ・ AC
弧PQの円周角 ∠PBQ = ∠PCQなので、
△PRB∽△QRC ⇒ PR:QR = RB:RC
△AQB∽△APC ⇒ AQ:AP = AB:AC