自然対数の底　eについて

　このところ指数・対数の話が続いているが、ｅについて。
　ここで言うｅは、電子のｅではなく、自然対数の底（てい）と呼ばれているｅ。

　思えば、始め10だったlogの底（常用対数の底）が、ある時から省略されるようになり、ある時からｅになり、また、ある時からlnが使われるようになり、幾度か振り回されてきた。
　log₁₀ x　－　log x
　log x　－　log_e x　－　ln x
　　※　log_e x ＝ ln x。lnはnatural log

　たいした説明もなく（聞いていなかっただけかもしれないが）突如現れたｅは2.718……という半端な値で、分数の形に表せない無理数。
　扱いづらそうな値なのに度々現れる。
　「自然」という名が付けられているが、その現れ方は不自然であった。

　幸いｅが何であるのか分からなくても使うことができる。
　y＝a^xをxについて微分したとき、a^xになるaの値が2.718……（＝e）。

　つまり、
　y’＝(d/dx)e^x ＝ e^x

　ちなみに

• 　(d/dx)x^a ＝ ax^a－1
• 　(d/dx)a^x ＝ (log_e a)a^x

　上の式は学び始めに登場する。例えば、x³をxについて微分すると3x²。

　y＝2^x、3^x、10^xを各々xについて微分すると
　(log 2) 2^x ≒ 0.69 × 2^x
　(log 3) 3^x ≒ 1.10 × 3^x
　(log 10) 10^x ≒ 2.30 × 10^x
になる。
　(log 2.718) 2.718^x ≒ 1 × 2.718^x

　ありとあらゆる数（真数）は、底のとり方によって無数に対数を作ることができる。
　例えば10の場合、底が２ならば3.32、ｅならば2.30、10ならば１、……。

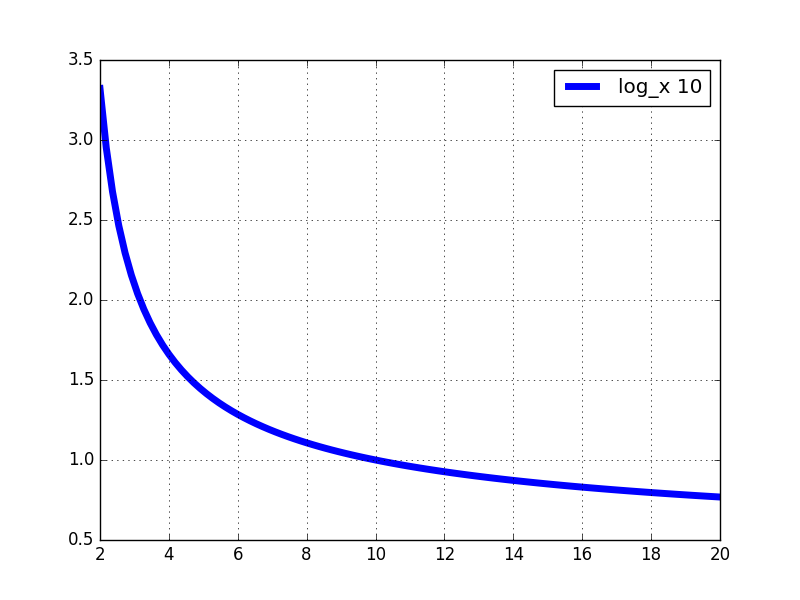
　底が何であっても構わないのであれば、微分（および積分）の際、何を使うか　－－－　ｅを使うが良いであろう。

　一般に
　e ＝ lim_n→∞(1＋1/n)ⁿ
と説明される。ｅの定義の１つ。

　n=1のとき(1＋1/n)ⁿ＝2
　n=2のとき(1.5)²＝2.25
　n=3のとき(1.33…)³＝2.37
　n=4のとき(1.25)⁴＝2.44
　n=5のとき(1.2)⁵＝2.49
　・
　・
　・

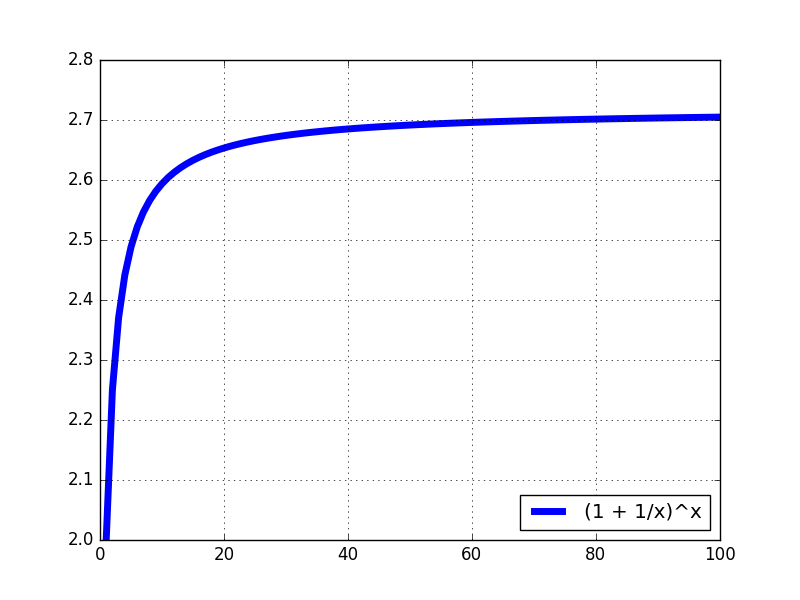
　n=10のとき(1.1)¹⁰＝2.59
　n=74で2.7を超え、n→∞で2.718……に収束する。

　ついでながら
　e^x ＝ lim_n→∞(1＋x/n)ⁿ
　e^-1 ＝ lim_n→∞(1－1/n)ⁿ ＝ 0.368

ｅの歴史と対数表

　歴史的には意外なことに対数は指数とセットで考案されたわけではなく、対数のほうが先んじていた－－－。
　自然対数の底　ｅは、ネイピア数もしくはオイラー数とも呼ばれているが、ネイピアが対数の概念を考案し、対数表を作った。
　その後、17世紀後半、ベルヌーイが利子の計算から (1＋1/n)ⁿの極限値2.718……に辿り着き、
　18世紀にオイラー（この人天才）がｅという記号を使うようになり、(d/dx)e^x ＝ e^xであることを示し、－－－
という順。
　ネイピアが2.718……を求めたわけではないが、ネイピア考案の対数に現れる。

　　※　ネイピアとは別にビュルギという人も同時代、独自に対数の概念を考案していた
　　　　小数点を用いた今日の小数の表記はネイピア以降

　使いやすい底10のlogの表（＝常用対数表）を作ったのは、ネイピアではなく少し後のブリッグスという人だが、今はコンピューターがあるので誰でもすぐに作れる。

　Excelで
　B1、C1、…、K1列に0.00、0.01、…、0.09
　A2、A3、…、A91行に1.0、1.1、…、9.9
と入力。
　B2に計算式「=LOG($A2+B$1,10)」を入力してセルコピー　⇒　右へ下へ各列各行K91までペースト。
　数（真数）1.00－9.99の常用対数の表出来上がり。

　そもそもコンピューターがあるなら対数表を使う必要はないが、まだコンピューターがなかった時代を想像しながら使ってみよう。

　例えば、6729 × 5483ならば、対数表の6.73と5.48を読んで
　log₁₀ 6.73 ＋ log₁₀ 10³ ＝ 0.828 ＋３
　log₁₀ 5.48 ＋ log₁₀ 10³ ＝ 0.739 ＋３
　各々足し合わせると1.567 ＋ 6 ＝ 0.567 + 7
　再び対数表で0.567に近い数（真数）を探すと3.69なので、
　3.69 × 10⁷ ＝ 3690万になる。
　（コンピューターで計算すると36895107）

　※　log xz ＝ log x ＋ log z

　0.6729 × 0.5483ならば、同じ要領で
　1.567 － 2 ＝ 0.567 － 1
　3.69 × 10^-1 ＝ 0.369

　6729 ÷ 5483ならば、
　0.828－0.739＝0.089に近い真数を対数表で探すと1.23。

　※　log x／z ＝ log x － log z

　桁数の大ーきな数同士の掛け算（割り算）が対数表を使う足し算（引き算）で済む。
　対数表のおかげで航海、天文におけるsin、cosなどの値　0.××××同士の乗除計算が楽になる。
　コンピューターがなかった時代のコンピューター的存在。

　■　オマケ

　ネイピアは16－17世紀の人。
　明智光秀と同じ時代。

blogふシゼンは１歳
log（ふシゼン）^b＝１歳（１サイクル）
（ふシゼン）^b＝e^１c＝e^c
（ふシゼン）^akb38＝e^akc38≒ 明智３日