指数と対数　その２　＋　累乗と累乗根　－　対数グラフ

　その１はこちら。
　指数と対数が逆関数の関係で、
　対数　logの足し算（引き算）は指数の掛け算（割り算）に対応する、という内容。

　log_k xz ＝ log_k x ± log_k z
　k^x±z ＝ k^x × k^±z

　底のｋが１未満の場合（0＜k＜１）の場合も同じだが、減っていく。
　y＝(1/2)^xは、例えば半減期のグラフ。

　k＝0は、普通は０のままだが、0^０＝1とすることが多い。
　ｋが負の数の場合（k＜0）、掛け合わせることはできるが、普通は考えない。

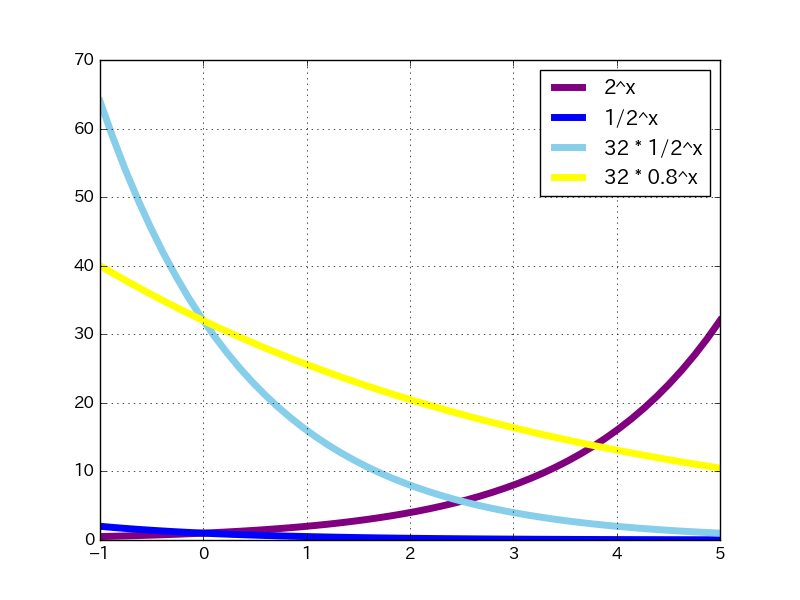
　Pythonのコード

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-1,5,50)
y2 = 2**x
y4 = 1/2**x
y5 = 32*1/2**x
y6 = 32*0.8**x
plt.plot(x,y2,"-",color="purple",lw=5,label="2^x")
plt.plot(x,y4,"-",color="blue",lw=5,label="1/2^x")
plt.plot(x,y5,"-",color="skyblue",lw=5,label="32 * 1/2^x")
plt.plot(x,y6,"-",color="yellow",lw=5,label="32 * 0.8^x")
plt.legend()
plt.grid()
plt.show()

　y=k^xは曲線になるが、対数を使えば、
　log y = log k^x ＝ log k × x
となり、「log yはxに比例する」と言って直線に変えられる。
　もしもy=αk^xならばlog y ＝ (log k)x ＋ log α

　指数のグラフに

plt.yscale("log")

を加えるとy軸が対数目盛になって直線の片対数グラフになる。

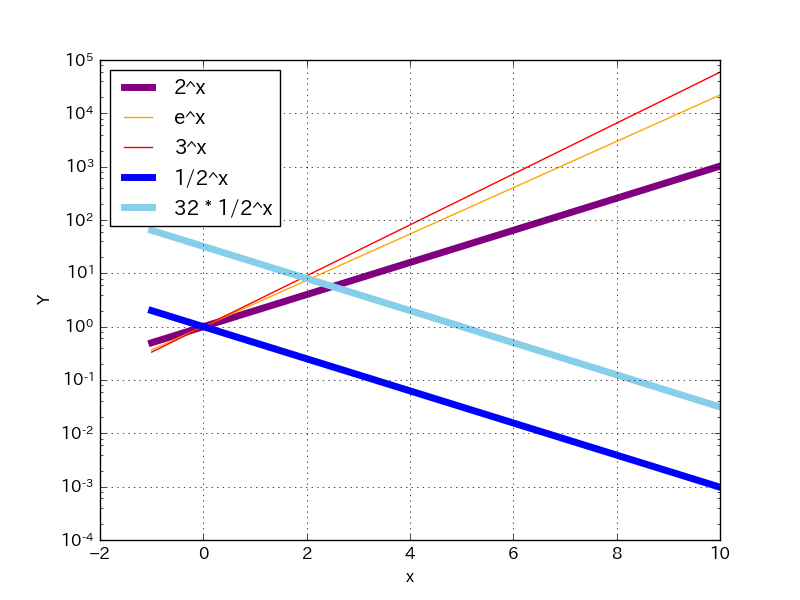
　Y＝log₁₀ yで、

　Y ＝ (log₁₀ 2)x ≒ 0.301x
　Y ＝ (log₁₀ e)x ≒ 0.434x
　Y ＝ (log₁₀ 3)x ≒ 0.477x
　Y ＝ (log₁₀ 1/2)x ≒ －0.301x

　Y ＝ (log₁₀ 2)xとY ＝ (log₁₀ 1/2)xがY＝０すなわちy＝10⁰＝１に対して対称になっている。
　Y ＝ (log 1/k)x　⇒　Y ＝－(log k)x。
　一般にy＝f(x)とy＝－f(x)はy＝0に対して対称。

累乗と累乗根

　今度はy=x^kの場合。
　k^xと同じく累乗の形だが、ｘは指数ではなく底。
　k=2ならば２次、k=3ならば３次、……のｋ次の式。
　逆関数はlogではなく、x＝y^1/k。
　指数が分数の形になる。

　例えばy=x^1/2の場合、三角形を描くと現れる平方根（２乗根）で、ルートｘ　√x。
　y=x^1/3の場合、立方根（３乗根）　³√x。
　y=x^1/nの場合、ｎ乗根　ⁿ√x。
　ｎ乗根はｎ乗するとｘになる数。

　例えばy=x^3/4ならば⁴√x³
　これら累乗根。

　なお、ルート（根号）の記号は正しくは、

$$ \sqrt{x}、\sqrt[3]{x}、\sqrt[n]{x}、\sqrt[4]{x^3} $$

　√5はPython　Numpyでnp.sqrt(5)。
　5^³は5**3もしくはpow(5,3)。Numpy不要。Excelだと5^3もしくはpower(5,3)。

　y=x^kは曲線になるが、対数を使えば、
　log y = log x^k ＝ log x × k
となり、「log yはlog xに比例する」と言って直線に変えられる。
　もしもy=αx^kならばlog y ＝ k(log x) ＋ log α。
　「yはx^kに比例する」　⇔　「log yはlog xに比例する（比例定数k）」

　例えばy＝3x²、y＝2x³、y＝√xのグラフに

plt.xscale("log")
plt.yscale("log")

を加えるとx軸、y軸が対数目盛になって直線の両対数グラフになる。
　サブプロット　subplotを使う場合は、set_xscale("log")、set_yscale("log")。

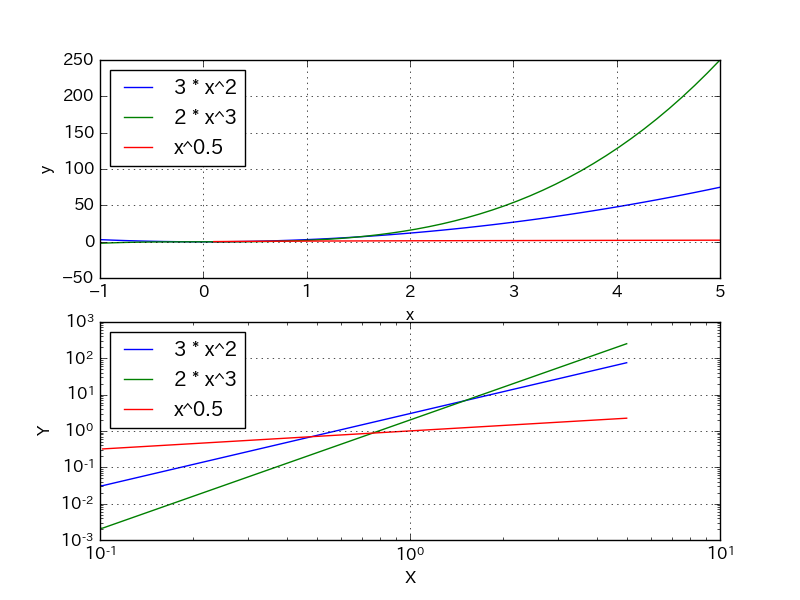
ax1 = plt.subplot(2,1,1)
ax2 = plt.subplot(2,1,2)
x = np.linspace(-1,5,50)
z = 3*x**2 
z2 = 2*x**3
z3 = np.sqrt(x)
ax1.plot(x,z,"-",label="3 * x^2")
ax1.plot(x,z2,"-",label="2 * x^3")
ax1.plot(x,z3,"-",label="x^0.5")
ax2.plot(x,z,"-",label="3 * x^2")
ax2.plot(x,z2,"-",label="2 * x^3")
ax2.plot(x,z3,"-",label="x^0.5")
ax1.legend(loc="upper left")
ax2.legend(loc="upper left")
ax2.set_xscale("log")
ax2.set_yscale("log")
ax1.set_xlabel("x")
ax1.set_ylabel("y")
ax2.set_xlabel("X")
ax2.set_ylabel("Y")
ax1.grid()
ax2.grid()
plt.show()

　y=x^kではなくy=x^k ＋ …… ＋ x + αになると
　いわゆるｋ次方程式を解くことになり、難しくなっていく。

　ｘが負の数の場合（x＜0）、普通は考えない。虚。
　だが、ｋ次の方程式を真面目に解こうとすると考えないわけにもいかない。
　２乗すると－１になる数すなわち虚数　ｉが導入されるのであった。