指数と対数について　－　グラフ描画

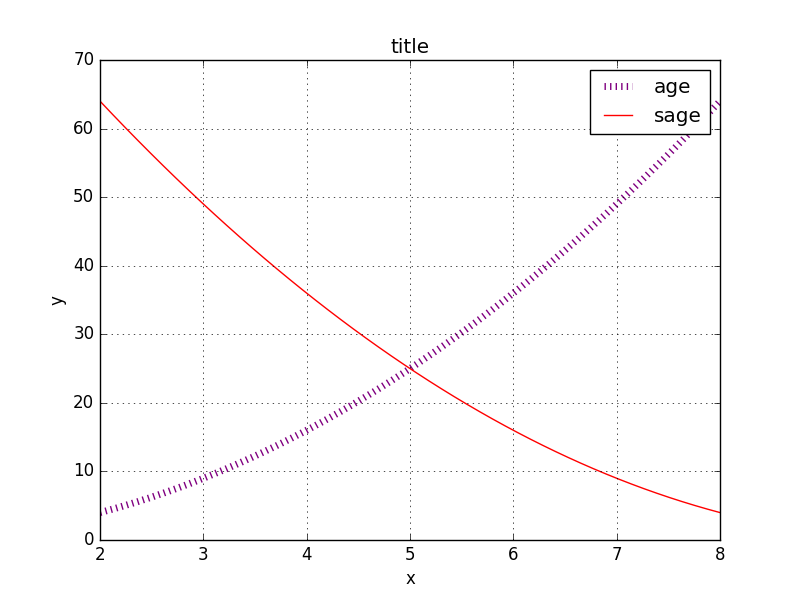
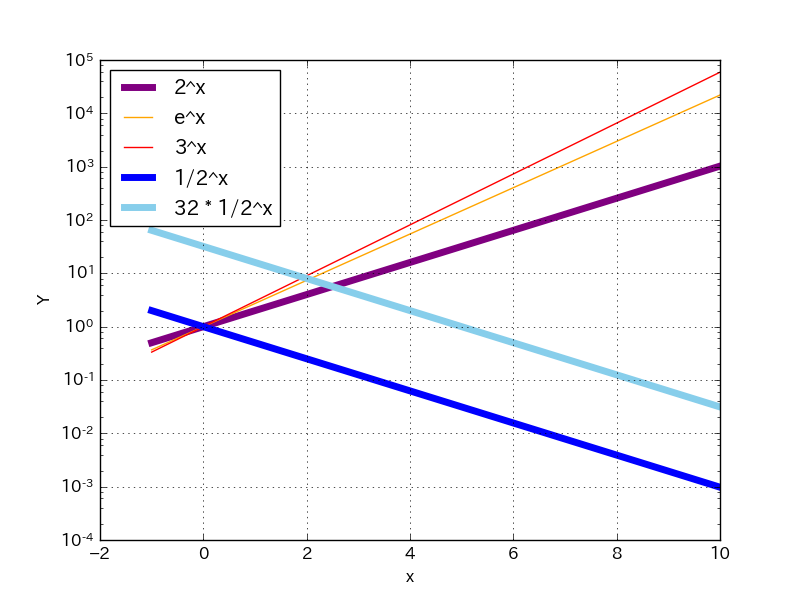
　大ーきな数、小ーさな数の扱い方。
　1000を10×10×10＝10³、100万を10⁶、10億を10⁹と表して、10³×10⁶＝10⁹といった計算が指数計算。
　例えば5の5乗は、5×5×5×5×5で、5⁵。
　Excelだと5^5、Pythonだと5**5。Ｒ言語はどっちでも。
　Excelだと5^5^5で、3125^5　→　2.980E+17（＝2.980×10¹⁷）
　Pythonだと5**5**5で、

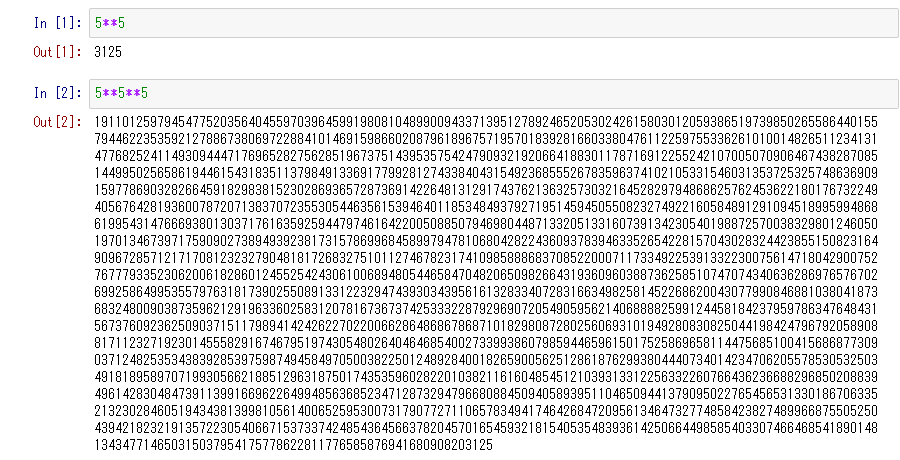
　オーマイ５－。3125の5乗ではなく5の3125乗で、2000桁超（2185桁）になる。超ー無量大数。Ｒ言語もPythonと同じだが、返り値はInf。Infinity＝無限大　∞。
　5の100乗が7.889E+69（＝7.889×10⁶⁹）。70桁。無量大数。
　Python　Jupyterの場合、

%precision %.3E
5.0**100

で小数点以下３桁までのE+表記になる。

%precision

で元通り。　

　kのx乗　－－－　y＝k^x。
　kの0乗　－－－　y＝k⁰＝1。
　kの-x乗　－－－　y＝k^-x＝1／k^x。
　これら累乗（冪べき乗）。kが底（てい）。xが指数。
　kが同じならば、
　k^x × k^z ＝ k^x+z
といった具合にまとめられる。
　k^x-z ＝ k^x × k^-z ＝ k^x ／ k^z
　10^ｰ3／10^ｰ6＝10³
といった具合。
　k^xz ＝ (k^x)^z

　指数の逆関数が対数。
　逆関数とは、まあ、逆です。例えば、y=kxの逆関数は、x＝y／k。比例が反比例になるわけじゃない。
　y＝k^xもx=～の形にすればよいのだが……。
　logという記号を使って
　x＝log_k y
となる。
　ログはログでもblogのlogではなく、logarithmの略。
　突如妙な記号が現れて、だんだん消化不良を起こし始める。

　0＝log_k 1
　1＝log_k k
　n log k＝log kⁿ

　log xz ＝ log x ＋ log z
　log x／z ＝ log x － log z
は、
　log k^x・k^z ＝ (x＋z)log k、log k^x ＝ x log k、log k^z ＝ z log k
といった具合に確かに成り立つ。

　x=10、z＝2とか値を入れてみる。

import numpy as np
np.log(5)

　＝1.6094379124341003
　np.log(10)＝2.3025850929940459
　np.log(2)＝0.69314718055994529
といった具合。
　コンピューターのおかげで気軽に計算できる。

　底のkが省略されているlogの場合、k=10かk＝e。
　log₁₀は常用対数、log_eは自然対数。
　上記のnp.log()は、k=e。約2.7。
　log₁₀ 2は、np.log10(2)＝0.3010299956639812。
　k＝2の場合、np.log2()。

　NumPyライブラリは、底が2、10、eの場合しか対応した関数がない。
　Python標準ライブラリのmathモジュールなら、ある。
　例えばlog₃ 10の場合、

import math
math.log(10,3)

　＝2.095903
　ExcelやＲ言語もlog(10,3)。

　Numpyライブラリの場合、底の変換公式と呼ばれる
　log_a b ＝ log_c b／log_c a
を使う。底のcは何でもよいので、
　log₃ 10 ＝ log 10／log 3　

import numpy as np
np.log(10)/np.log(3)

で、＝2.095903。

グラフ

　下図は指数のグラフ。

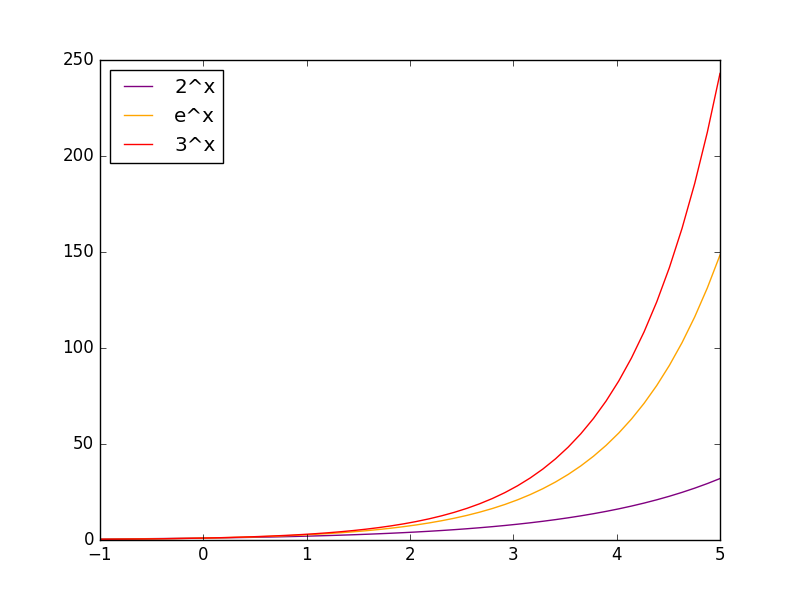
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-1,5,50)
z2 = 2**x
ze = np.e**x
z3 = 3**x
plt.plot(x,z2,"-",color="purple",label="2^x")
plt.plot(x,ze,"-",color="orange",label="e^x")
plt.plot(x,z3,"-",color="red",label="3^x")
plt.legend(loc="upper left")
plt.show()

　x＝0でy＝1。x＜0のときy＜1。y＝0にはならない。

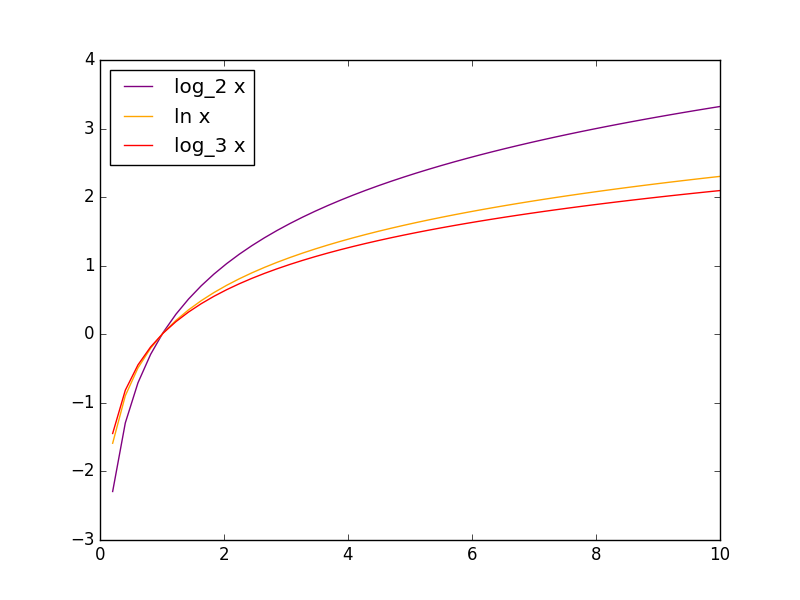
　下図は対数のグラフ。

x = np.linspace(0,10,50)
z2 = np.log2(x)
ze = np.log(x)
z3 = np.log(x)/np.log(3)
plt.plot(x,z2,"-",color="purple",label="log_2 x")
plt.plot(x,ze,"-",color="orange",label="ln x")
plt.plot(x,z3,"-",color="red",label="log_3 x")
plt.legend(loc="upper left")
plt.show()

　log_e 2、log_e e、log_e 3、……のlog_e x（＝ln x）など対数の曲線も右上がりだが、指数の曲線とは異なる。
　x＝1でy＝0。x＜1のときy＜0。x＝0にはならない。

　つづく。