以前、日本の過去10年間の大地震(「最大震度6強以上」)についてプロットしたが、今回は世界の過去10年間の大地震についてプロットしてみた。
日本の地震は気象庁のデータを利用したが、
世界の地震はUSGS(アメリカ地質調査所)のデータを利用。
USGSは日本の国土地理院のように地形図を作成しているところ。
マグニチュード6以上
まずUSGS Earthquake Hazards Program(earthquake.usgs.gov/)にアクセス。
Latest Earthquakesで、直近24時間に起こったマグニチュード2.5以上(M2.5+)の地震震源情報、地図表示。
Search Earthquake Catalogで、規模、期間、地域を選択して表示。
今回、
- 規模 = マグニチュード6以上(M6+) ・・・ CustomのMinimumを6
- 期間 = Start 2011-01-01~End 2021-05-30
- 地域 = World(世界)
を選択して検索 Search。
検索結果 Search Resaltsは、1516データ。
画面左のリストの一番下からダウンロード DOWNLOADできる。
データ形式はCSV、GeoJson、KML、QuakeML。
Leaflet + OpenStreetMapでプロットされているので、改めてプロットし直す必要はないが、せっかくなのでGeoJSONデータをダウンロードしてプロット。
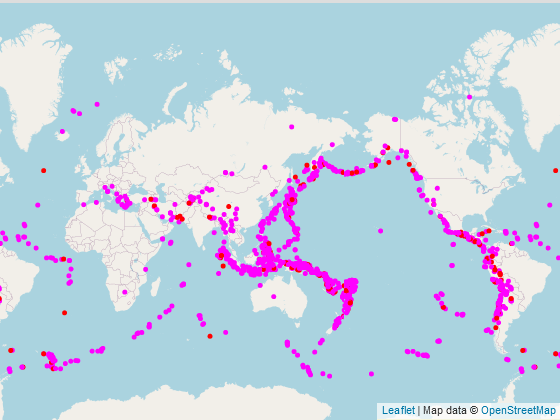
気象庁のマグニチュードとUSGSのマグニチュードはやや異なる。
マグニチュード5以上
もっとたくさんプロットすべくマグニチュード4.5以上(M4.5+)で検索したら極端に増えて78152データ。
20000データが限度。
マグニチュード5以上(M5+)で検索したら限度内の18446データ。
マグニチュード Mと地震の発生頻度 Nの関係式は、
log10 N = a - bM
グーテンベルク-リヒターの関係式(G-R式)。印刷のグ氏とは別人。
この式は以前こちらのページで触れたマグニチュード Mと地震のエネルギー Eの関係式
1.5M + 4.8 = log10 E [J]
と同じ片対数の形式。傾きが違う。
Mが増減 ⇔ Eが指数関数的増減
Mが増減 ⇔ Nが指数関数的減増
という式。
log10 N’ = a - bM’
log10 (N’/N) = log10 N’ - log10 N = b(M-M’) ・・・ aが消える
N’/N = 10b(M-M’)
で、b値は0.9~1.0、とのこと。
よってM-M’=1、つまりMが1小さくなると発生頻度10b倍(約8~10倍)、Mが2小さくなると102b倍(約63~100倍)。
Mが1.5小さくなると101.5b倍(約22~約32倍)。
18446/1516 = 12.17。
仮にb=1.1ならば12.6倍。
78152/1516 = 51.55。
仮にb=1.15ならば53倍。
まあ、こういうこともある。
気を取り直してM6+同様、M5+もプロット。
GeoJSONファイルのサイズも11倍(10MB超)なのでプロット画像だけ。
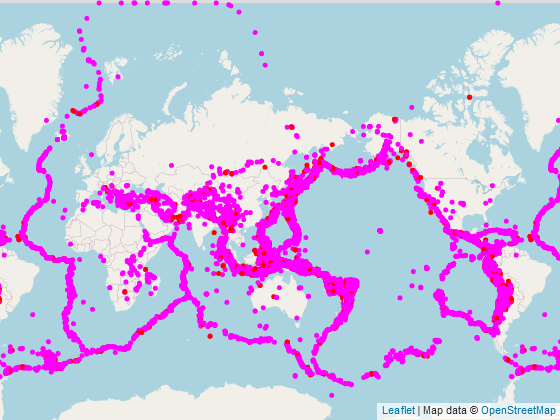
プレート境界が描かれたも同然。
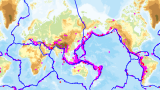
なお、USGSの地図にはプレート境界が赤線で描かれている。
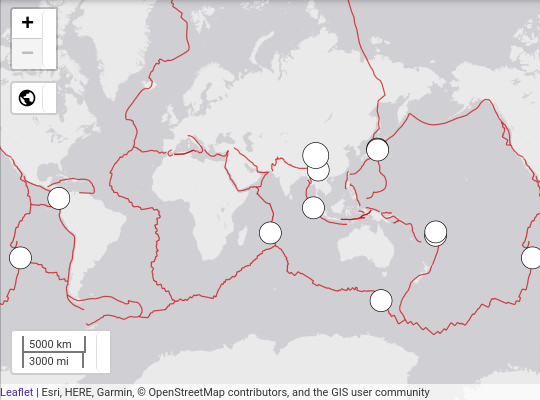
続く。