地震ぐらぐら
最近あまり地震がない、と思っていたら起きた。
マグニチュード7.3(M7.3)。
震度6強
宮城県蔵王、山元
福島県相馬、国見、新地
震度6弱
宮城県石巻、岩沼、登米、川崎、亘理、利府、南三陸
福島県福島、郡山、須賀川、南相馬、伊達、本宮、桑折、川俣、天栄、矢吹、三春、広野、楢葉、川内、大熊、双葉、浪江、葛尾
※ 上記震度は防災科学技術研究所 J-RISQ 地震速報(www.j-risq.bosai.go.jp/report/)から
橙字は気象庁発表の震度と一致していない
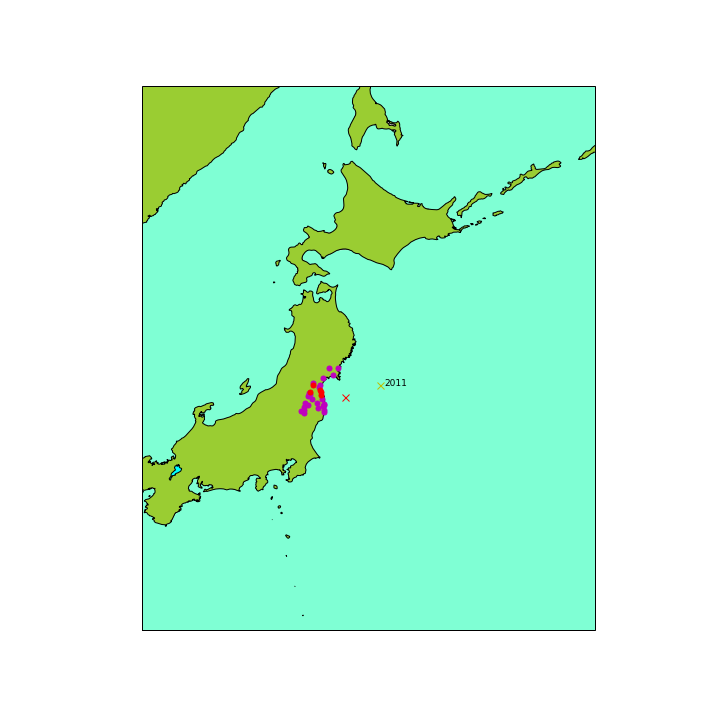
最大震度5強 栃木
最大震度5弱 岩手、山形、茨城、埼玉
神奈川は最大震度4。ぐらぐら揺れて、通常だったら収まるはずの頃合から逆に揺れが強くなっていく長い地震。
2011年3月の東日本大震災を思い出した。当時はもっとぐんらんぐんらん大きく揺れたが、まだ大きくなるのかーと思いながらも何となく震源は近くない感じがした。そして、思った。震源の近くは、もっと酷く揺れたのではあるまいか。これ以上の揺れがあるとしたら……。速報を見るのが恐怖だったことを覚えている。その後の津波、原発事故が酷かったが。
今回は発生時刻がPM11:08。速報見た時がPM11:11。
早い段階で津波発生の恐れなしの報。
震源の深さ約55km。
一般に震源が浅いと被害も大きくなるが、ギリギリ津波は発生しなかった、とのこと。
東日本大震災の時は震源の深さ約24km。
M7.5、深さ50kmだったら津波が発生していた、ということか。
大地震・大津波は1度起きたら当分の間起きないものと思っていたが、そうとも言えないようだ。
東日本大震災の後、そろそろ10年経つが、まだ余震だという。マグニチュード7超でも余震。
大震災以前は、こういった使われ方をしていなかった(と思う)用語なので、少し違和感を覚えるが、M8超、M9の巨大地震は特別な地震ということなのだろう。
日本列島毎年地震ゼロというわけにはいかないから、小さい地震がちょくちょくあったほうが幾分マシなのかもしれない。
マグニチュード Magnitude
このところ指数・対数の話を続けている。
『地震の規模を示すマグニチュード』が対数利用の実例なので小まとめ。
地震のついでではなく地震がついで。
一口にマグニチュードと言ってもいろいろ種類があって難しそうだが、基本的には
マグニチュード M = log A + B
の形の式。
Aは地震波の最大振幅などから。
Bは補正項で、震央距離や震源の深さなどから。
BはB=log10 10Bとかlog2 2B とか変形できるので、log Bでもよいが、
10M=A × 10Bの常用対数がM = log A + B。
10M=A × Bの常用対数がM = log A + log B(=log AB)。
10Mの場合、Mが1大きくなると10倍、2大きくなると100倍で、桁違いの大きさになるが、
実際にはMが1大きくなると約31.6倍、2大きくなると1000倍で、もっと桁違い。
約31.6のM乗。つまり、logの底が約31.6(=√1000)。
この値は、
マグニチュード Mと地震のエネルギー Eの関係式
1.5M + 4.8 = log10 E [J]
から得られる。
※ [J]はエネルギーの単位・ジュール
単位がエルグ [erg]だと
1[erg]=10-7[J]で、log10 E [J]=log10 (E×10-7) [erg]になるので、4.8が11.8になる。
1.5M’ + 4.8 = log10 E’
log10 (E’/E) = log10 E’ - log10 E = 1.5M’-1.5M
E’/E = 10 1.5(M’-M)
で、M’-M=1、つまりMが1大きくなるとエネルギー101.5倍(約31.6倍)、Mが2大きくなるとエネルギー103倍(1000倍)。
MとEの関係式を変形すると
M = log10 E/1.5 - 4.8/1.5
底の変換 log10 E = logx E/logx 10
で、logx 10=1/1.5となるx(x1/1.5=10となるx)は101.5(=√1000)
M = log√1000 E- 3.2
今回の地震がM7.3、2011年の地震がM9.0なので、2011年は今回の102.55=約355倍のエネルギー。
※ 1.5 × (9-7.3)=2.55
2011年のM9.0はモーメント・マグニチュード Mwの値。求め方が異なる
M7.3のときE=5.623×1015[J]、M9.0のときE=1.995×1018[J]で、両者の比は約355。
追)MからE、比の計算 →