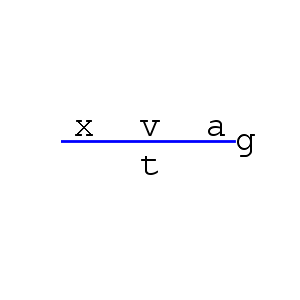物理の初め、力学の初め、
距離 x = 速度 v × 時間 t
のまとめ。
実際には力学の初めは、物体の大きさ、重さ、力の釣り合いなどを論じた速度0(v=0)の静力学 statics。古代から精巧な建造物、巨大な建造物が造られている。
v≠0が動力学 dynamics。
物体の運動に関する理論は中世に新たに生まれて、以降、更新されていった。古来の感覚的な理解が観測・実験から得られる事実と違っていた。
速度 velocity
速度 vは距離÷時間
v= x/t
単位はm/s、km/hなど
km/hの値に5/18をかけるとm/sの値
80[km/h] = 80 × (1000[m]/3600[s]) = 80 × (5/18) = 22.222[m/s]
逆に30[m/s]は30 × (18/5) で108[km/h]
時速50kで30分、時速30kで50分走りました。
平均時速は40k?
--- 全体の距離は、50[km/h] × (30/60)[h] + 30[km/h] × (50/60)[h] = 25 + 25 = 50[km]
全体の時間は80分(= 80/60[h] = 1.333[h])
全体の距離÷全体の時間 = 37.5[km/h]
でした
速度はより厳密には移動距離(変位)÷経過時間
v=Δx/Δt
微小変化は、
lim Δt→0で、v = dx/dt ・・・ xをtで微分(瞬時の変位量)
加速度 acceleration
加速度 aは速度÷時間
単位はm/s2など
aが+ならば加速
aが-ならば減速
地震の際に見掛ける単位ガル galは、
1[gal] = 1[cm/s2] = 0.01[m/s2]
加速度は変化した速度÷経過時間
a=Δv/Δt
微小変化は、
lim Δt→0で、a = dv/dt = (dx/dt)/dt = d2x/dt2 ・・・ vをtで微分(瞬時の変速量) = xをtで2回微分
直線運動(等加速度 a=一定)
物理は数学と不可分で、微分・積分が混じることもあるが、ひとまず式を変えていく。
dx = v dt
⇒ ∫dx = ∫v dt ⇒ x = vt + C(定数)
t=0の位置をx0とすればC=x0
⇒ x = vt + x0
dv = a dt
⇒ ∫dv = ∫a dt ⇒ v = at + C(定数)
t=0でC=v0(初速)
v = at + v0
床との摩擦、空気抵抗を無視すれば、
初速0、加速度5[m/s2]で10秒後の速度
v = 50[m/s]
上のv式をx = vt + x0ではなく
dx = v dtに代入
dx = (at + v0)dt
⇒ ∫dx = ∫(at + v0)dt ⇒ x = (1/2)at2 + v0t + C(定数)
t=0でC=x0
Δx = x - x0 = (1/2)at2 + v0t
床との摩擦、空気抵抗を無視すれば、
初速0、加速度5[m/s2]で10秒後の移動距離
Δx = 250[m]
初速0から1秒後に時速36k(=10[m/s])到達だと
a = v/t = 10[m/s2]
35[km/h]ちょっとで9.8[m/s2] = g(重力加速度) = 1G(ジー)
3秒後に105.8[km/h](=29.4[m/s])到達だと
a = 9.8 [m/s2] = 1G
1秒後に106[km/h]到達だと3G。
時速120k(=33.333[m/s])から3秒で急停止(速度0)だと
0-33.333 = a×3
a = -11.111[m/s2]
Δx = -50+100 = 50[m]
いろいろ値を入れているうちに理数が好きになる
か?
ならないか
なお、加速度0(a=0)のときは等速[度]直線運動
v = v0
Δx = x - x0 = v0t
自由落下、
水平方向ではなく鉛直方向の直線運動も基本的に同じ。
地上における自由落下や投げ上げ運動において物体にかかる加速度は、
重力加速度 g = 9.8[m/s2]。
たいてい座標はy方向の上を+にとるので、下向きにかかるgは-。
a=-g
(y方向の下を+にとれば、a=g)
v = -gt + v0
Δy = y - y0 = -(1/2)gt2 + v0t
空気抵抗を無視すれば、
初速0、高さ330mから地上に落下するまでの時間
0-330 = -0.5×9.8t2
t=8.2[s]
地上落下時の速度
v=-80[m/s]=-290[km/h]
高さ630mからだと
t=11.3[s]
v=-111[m/s]=-400[km/h]
感覚的には重いもののほうが早く落ちそうに思えるが、
重いものも軽いものも落下時間、落下速度は同じ。
16世紀末、イタリアのピサの斜塔にて、若かりし頃のガリレオ・ガリレイによって確かめられた。