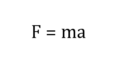もう1回物理力学。
振動それはバイブレーション Vibration。
糸でつり下がった物体がゆらゆら右へ左へ揺れる単振り子。
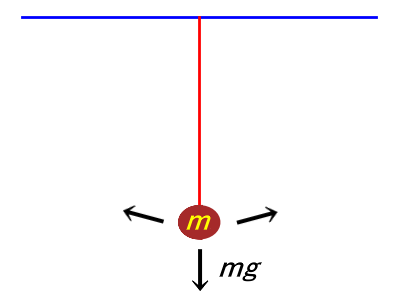
ここで着目するのは鉛直方向ではなく水平方向だが、物体は直線運動ではなく弧を描く。
勢いよくブーンと回せば円運動になる。
行って戻って、往復したり(振動)、回転する場合、1サイクルの時間を周期と呼ぶ。1サイクル360°(=2π)。
ガリレオはこの振り子の周期が物体の重さ(実際は質量)によらないことを見抜いた。等時性。
ニュートンも振り子の実験を数多く行った。
周期 T = 2π √(l/g)
・・・ 定式化したのはガリレオの後、17世紀のホイヘンス。波の伝播などで名前を見かける。振り子時計の発明者。
周期は物体の質量 mによらず、糸の長さ lで決まる。
糸が長いほど周期が長い。
単振動
一般に物体に復元力 -kxがかかる場合、バネ付きの物体に代表されるように行ったり戻ったり振動する。弾性体。
F = -kxは、フックの法則。
フックはニュートン、ホイヘンスと同時代。しばしばニュートンの宿敵と紹介される。
k:バネ定数。弾性係数の一種。
物体の自由落下の運動方程式は、
ma = mg
a = gで、等加速度運動。
v= gt + v0
x = (1/2)gt2 + v0t。
・・・ a = d2x/dt2
d2x/dt2 = gの微分方程式を解いた結果(2回tで積分した結果)
一方、振動(単振動)は加速度が変化する往復運動。
運動方程式は、
ma = -kx
簡素に見える式だが、
微分方程式 m(d2x/dt2)= -kx(k>0)
のxはsin、cosの式になるのでした……
・・・ ちなみにm(d2x/dt2)= kx(k>0)だとxは自然対数 eの式になる。
なぜなのだ?としばらく考え込んだことがあるが、
とりあえず単振動の周期 Tは、
T = 2π √(m/k)
となる。
この単振動が媒体(大気中、水中など)を伝播していくのが波(波動)。
単振り子も単振動の一種だが、周期に物体の質量 mは関係しない。
・・・ 運動方程式は、糸(長さl)と鉛直方向の角度がθのとき、物体の運動方向(糸の方向と垂直、接線方向)に
ma = -mg sinθ
弧長 lθが変位 xに相当。a = d2(lθ)/dt2 = l(d2θ/dt2)
地震と振動
単振り子を反転して、糸の代わりに棒を立てると……
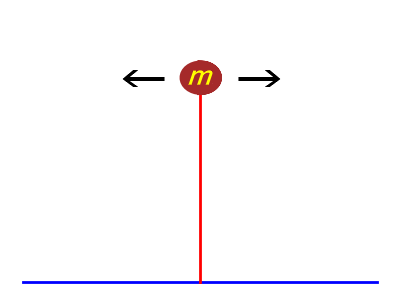
水平方向にゆらゆら右へ左へ揺れて、
強い力が加わると棒がポキッと折れる。
地震対策を考えるうえで、建造物の一番簡単なモデルも上の図。1質点1自由度。
棒の水平方向に復元力がかかって振動する。
単振り子は糸が長いほど周期が長かったので、
上のモデルも棒が長いほど周期が長そうに見える。
実際、低い家屋より高層ビルのほうが揺れの[固有]周期が長い。
ただ、(重力ではなく)復元力 -kxが作用する単振動の周期 Tは、
T = 2π √(m/k)
で、質量 mが大きいほど周期が長く、弾性係数 kが大きいほど(硬いほど)周期が短い。
(棒の)材料のヤング係数が弾性係数。
家屋、ビルなど建造物には各々固有周期があって、
高さ100m未満だと固有周期は2秒未満。
高さ200m以上の鉄骨造ビルだと概ね4秒以上。
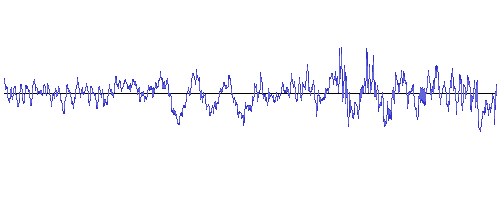
地震の揺れもいろいろあって、
強震観測データの波形を見るとより分かるが、
応答スペクトルのデータの山(ピーク)になっているところの周期(横軸)が、建造物の固有周期と重なり合ってくると揺れの振幅が大きくなる。共振。
※ 応答スペクトルには加速度、速度、変位がある
気象庁データに速度、防災科学技術研究所データに速度と加速度が掲載されている
速度は地震のエネルギー、加速度は地震の力に相当
周期1秒-2秒の「キラーパルス」が数多くの家屋倒壊を引き起こすと言われているが、
実のところ木造家屋の固有周期は1秒未満。
初期の強い揺れで柱や壁の硬さ(弾性)が失われて(塑性化)、だんだん固有周期が長くなって、1秒以上になりうる。
が、「キラーパルス」は周期1秒-2秒が卓越している揺れの中に含まれる継続時間の短い衝撃的なパルス[波]なので、
共振とは意味が異なる。
東日本大震災の時に首都圏で感じられた周期の長い揺れ = 長周期地震動は、100m、200m超の高層ビルと共振する。
単振動だとずーっと振動し続けるが、実際は摩擦力や空気抵抗などの抗力がかかって弱まっていく。減衰振動。
抗力をRとすると運動方程式は、
ma = -kx -R
建造物には固有周期の他、減衰定数(減衰率)がある。値が大きいほど弱まる。たとえば、減衰定数10%の場合、1周期ごとに揺れの振幅が10%減衰する。
気象庁データ、防災科学技術研究所データの応答スペクトルのh=5%、Damping=5%が減衰定数。
地震の力がかかる場合、強制振動。
地震[波]の周期と建造物の固有周期の差によって変わってくるが、差が0に近い(共振する)場合、揺れの振幅が大きくなっていく(増幅していく)。
運動方程式は、
ma = -kx + 地震力
もしくは
ma = -kx -R + 地震力
なお、運動方程式(微分方程式)は容易には解けない。