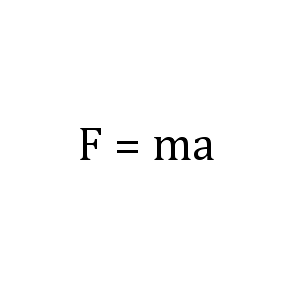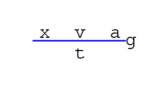このところ建造物にかかる力、地震(活断層、プレートにかかる力)、月面探査機、ロケットと物理の話題が続いたので、
動力学 dynamicsの初めの一歩のページを作成した。
力という概念はみな何となく知っている。
押したり、引いたり、
重力、浮力、抗力、推力、……。
力 Force = 質量 mass × 加速度
F = ma
質量もまあ分かる。時折重さ(重量)と混同したり、深く探ると分からない点もあるが、まあまあ分かる。
残るは加速度。
運動の法則
動力学の初めの初めの一歩は、
時間 t、距離(変位) x、速度 v、加速度 a
の関係から。
空気抵抗を無視すれば、物体の落下時間、落下速度は質量関係なく同じ。
空中から地面に向かう一定の加速度(重力加速度)を見出したのは中世、ガリレオ・ガリレイだった。
古来の感覚的な見方が実験と論証によって覆された。
v = x/t、a = v/tならば、
x = at2になるが、
v = dx/dt、a = dv/dtなので、
x = (1/2)at2 + v0t
v0:初速
になる。
微分・積分の計算法は、ニュートンおよび同時代のライプニッツが編み出した。
dv/dtは、とりあえず縦軸v-横軸tの曲線グラフを思い浮かべてみると良いかも。
ガリレオやニュートンの時代、16世紀-17世紀まで、既に航海術、鉄砲、望遠鏡など高度な技術があった。だが、運動する物体の刻一刻を精確に捉える術はなかった。
3法則
物体の運動に関する諸法則は、1687年、ニュートンの『プリンキピア PRINCIPIA(自然哲学の数学的諸原理)』にて体系づけられた。
うち運動の3法則は---
第1法則 慣性の法則
慣性とは
・ 止まっている物体は止まり続ける
・ 動いている物体は動き続ける
という性質。
ニュートンの少し前の時代のガリレオ、デカルトが導き出している。
デカルトは思弁的(哲学的)に。
ガリレオは実証的(科学的)に。
ガリレオは直線運動と考えていなかったようだが、
・ 動いている物体は、等速直線運動で、動き続ける。
もしも
・ 止まっている物体が動き出したり、
・ 動いている物体の速度が変わったりする場合、
外から何らかの力(外力)がかかっている
という理解になる。
もしも
動いている物体が曲がるならば(曲線運動)、何らかの外力がかかっている
という理解になる。
第2法則 [ニュートンの]運動の法則
加速度は物体にかかる力に比例する。
ガリレオは加速度が生じる原因について深く探らなかった。
質量ではなく重さを物体の(内在の)性質と捉えたため。
加速度と力を結びつけたのはニュートン。
加速度は物体の質量に反比例する。
a ∝ F/m
F = ma
日常眺めている世界においてはほぼ揺るがない土台(公理)。
力の単位はN(ニュートン)、kgf(キログラム重)。
1[N] = 1[kg・m/s2]
1[kgf] =9.8[N]。1000[N](=1[kN])ならば100[kg] ちょっとの重み。
ちなみに地震波の観測データで見かける加速度の単位 [ガル gal](=[cm/s2])の由来はガリレオ galileo。
F = maは、
a = dv/dtで、
F = m(dv/dt)
F dt = d(mv)
F dt:力積
運動量 p = mvで、
F = dp/dt
F dt = dp
とも記される。
第3法則 作用反作用の法則
物体Aが物体Bを押したり引いたりすれば、
物体Aは物体Bから押されたり引かれたりする。
同じ大きさの力で。
物体Aと物体Bから成る塊(系)を1つの物体とみなすことが可能。
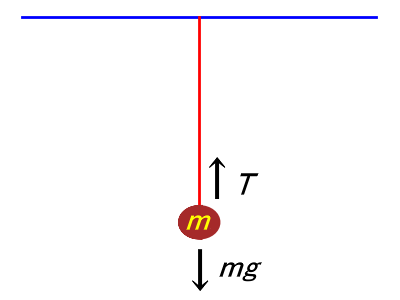
下図1の場合、
赤い糸が青天井を引っ張り(下向きの力 Tが作用)、
赤い糸は青天井に引っ張られる(反作用として上向きの力 T)。
力はベクトル。
物体にかかる力を図上でペタペタ矢印つける。
試験の問題で力の向きを間違えると誤った答えになる。めげない。
つり合いの式
動かないので作用反作用の法則と似ているが、2つの物体ではなく、1つの物体に着目する。
上図1の場合、
質量 mの物体に重力 mgと張力 Tがかかり、
mg = T
でつり合う。
運動方程式
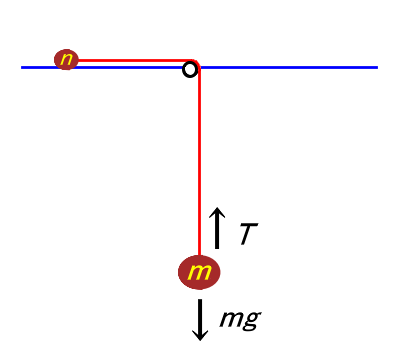
上図2の場合、下向きに+の加速度 aで動くとして、
・ 質量 mの物体
ma = mg - T
・ 質量 nの物体
na = T - 摩擦力
といった具合に式を立てる。
aやTが求まる。
運動方程式は微分方程式。速度 v、変位 xも求まる。