正距/正角
前回は日本地図にマーカーやテキストをプロットしたが、Cartopyをインストールして最初に描く(であろう)世界全図の場合、解像度は「110m」。
使い回し部分は以下のとおり。
import cartopy.crs as ccrs
import matplotlib.pyplot as plt
fig=plt.figure(figsize=(10,10))
ax=plt.axes(projection=ccrs.PlateCarree())
ax.coastlines(resolution='110m')
ax.gridlines(draw_labels=True)
plt.savefig("PlateCarree.png")
plt.show() インストールの回でも説明。
ax.coastlines(resolution='110m')は、ax.coastlines()でも同じ。
ax.gridlines()は、draw_labels=Trueで経線・緯線のラベルを付けてくれる。
下図が正距円筒図法 PlateCarree。
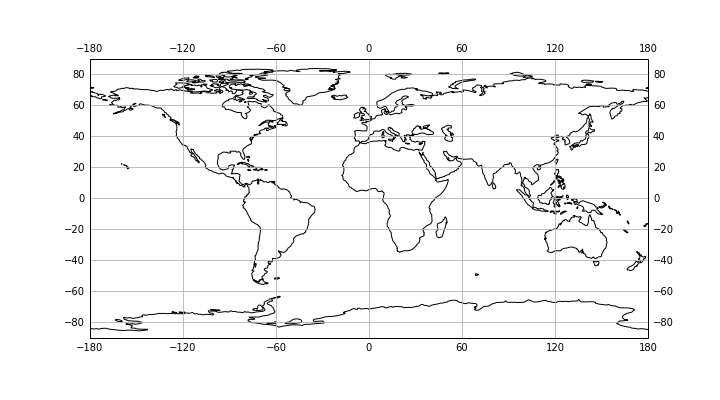
緯度、経度の範囲
ax.set_extent((-180.0, 180.0, -90.0, 90.0),ccrs.PlateCarree())を追加して
ax.plot(139.60,35.50,'mo',markersize='8')でプロット。
大陸と海の色塗りも追加して、今度はメルカトル図法 Mercatorで描画。
ax=plt.axes(projection=ccrs.Mercator())
ax.coastlines()
import cartopy.feature as cfea
ax.add_feature(cfea.OCEAN,color='#7fffd4')
ax.add_feature(cfea.LAND,color='#9acd32')
ax.gridlines(draw_labels=True)
plt.savefig("Mercator.png")
plt.show() OCEAN、LANDは小文字だとエラー。
経線・緯線のラベルは
ax.gridlines(ccrs.Mercator(),draw_labels=True)だとエラー。
メルカトル図法でプロットする場合、
ax.set_extent((-180.0, 180.0, -85.0, 85.0),ccrs.PlateCarree())
ax.plot(139.60,35.50,'mo',markersize='8',
transform=ccrs.PlateCarree()) ここはccrs.Mercator()ではなく
ccrs.PlateCarree()。
緯度は-90.0(南極)、90.0(北極)指定だとエラー。
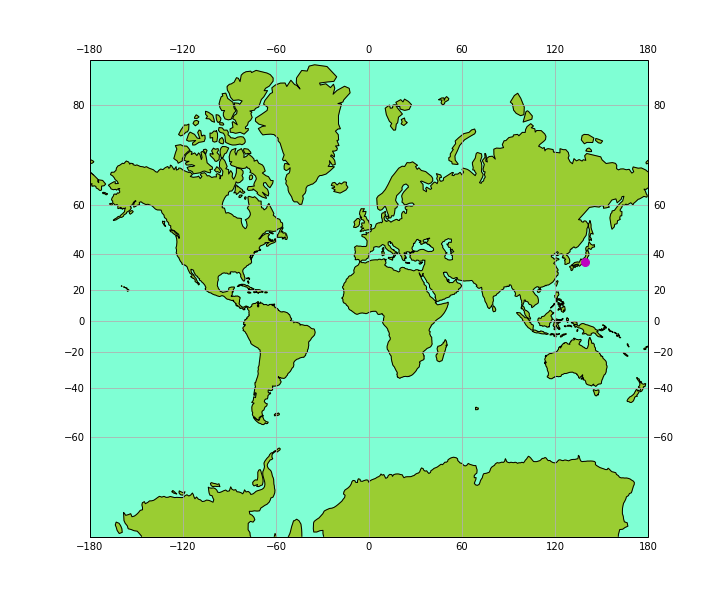
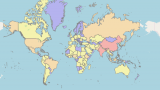
メルカトル図法は正距円筒図法を南北に引き延ばした図。こっちのほうが見慣れている。
※ オンライン地図でよく使われているのが球面メルカトル図法。
正距円筒図法の地図は南北方向の距離が正確で、緯度1°と経度1°を同じ距離としたもの。東西方向は赤道以外正距ではない。
メルカトル図法は東西も南北も正距ではないが正角。東西の拡大率と南北の拡大率が同じ。いわゆる相似。ただし、極点近くでは延びに延びて面積が極めて不正確。
正角というのが、これまたややこしい。以前、方角正確と書いたが(紛らわしいので消した)、遠方では正距方位図法で見る地球上の方位とは違ってくる。
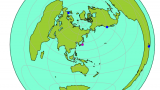
下図が正距方位図法。中心は緯度0°、経度0°のギニア湾。
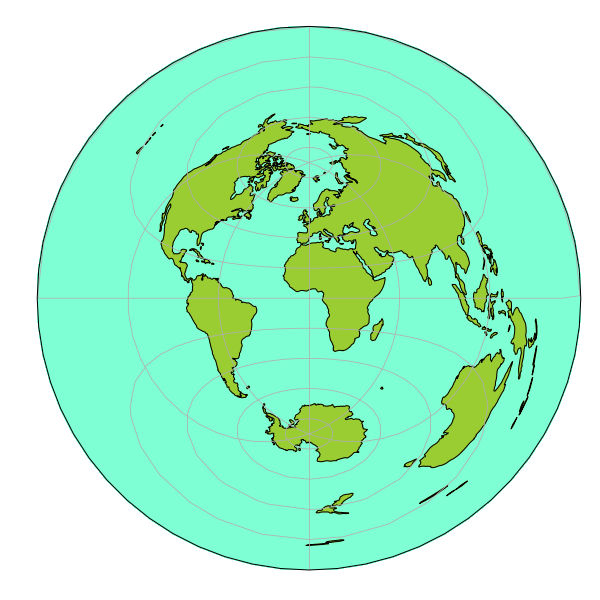
正積
距離、方角・方位、そして面積。
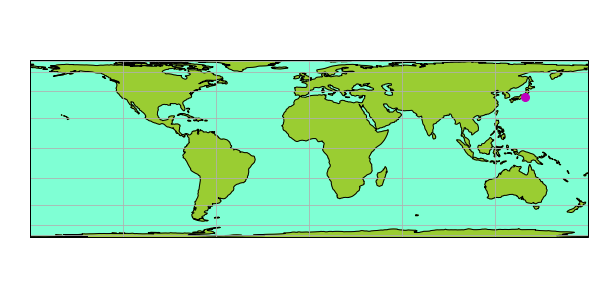
極点に近づくにつれて南北方向を縮めることで正積とした地図が[ランベルト]正積円筒図法 LambertCylindrical。
ax=plt.axes(projection=ccrs.LambertCylindrical()) ax.gridlines(draw_labels=True)だとエラー。経線・緯線のラベルがつかない。
追)最新バージョン(Cartopy 0.18)だとつくようだが試していない
ax.gridlines()プロットは、
ax.set_extent((-180.0, 180.0, -90.0, 90.0),ccrs.PlateCarree())
ax.plot(139.60,35.50,'mo',markersize='8',
transform=ccrs.PlateCarree()) ここはccrs.LambertCylindrical()ではなく
ccrs.PlateCarree()。
もう1つ代表的な正積図法は、モルワイデ図法 Mollweide。こちらは極点に近づくにつれて東西方向が縮んでいる。
メルカトル、ランベルト、モルワイデみな人名。
ax=plt.axes(projection=ccrs.Mollweide()) プロットは、ax.set_extent()でうまくいかず、ax.set_global()で全図描画。
ax.set_global()
ax.plot(139.60,35.50,'mo',markersize='8',
transform=ccrs.PlateCarree())
ax.gridlines() ここはccrs.Mollweide()ではなく
ccrs.PlateCarree()。
ax.gridlines(draw_labels=True)だとエラー。ラベルがつかない。
追)最新バージョン(0.18)だとつくようだ
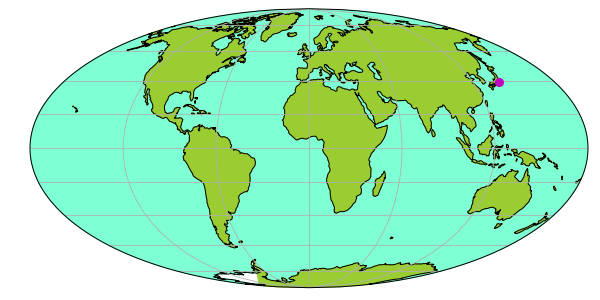
南極の西が色塗りできていないが不詳。
以上、正距方位図法以外みな円筒図法。