前回、三角形などの図形を描いて昔を思い出したので、
ついでにベクトルについて少しまとめてみた。
ベクトルという言葉自体は、専門用語の域を出て、時々使われているのを耳にするが、記憶を辿ると初出は高校の数学。
始めは矢印でABなどと表記されていたが、
やがて太字だけの表記が主流になった。
太字がベクトルで、細字がスカラー。
スカラーとは日頃使っている数量のことで、大きさや質量など。
ベクトルは大きさに加えて向きが備わる。
コンピューターで矢印つけようとすると少々面倒なので、以下太字で表記したが、念のため青字にしておいた。
ふりがな(ルビ)が使えるので、今回はルビに→を入力して済ませたが、心許ないので、こちらも青字にしておいた。
なお、MathJaxを使えばキレイに表示できる。
ベクトルの初歩
では、ベクトルの初めの一歩。
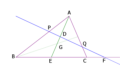
下の図の矢印は、みんなベクトル。
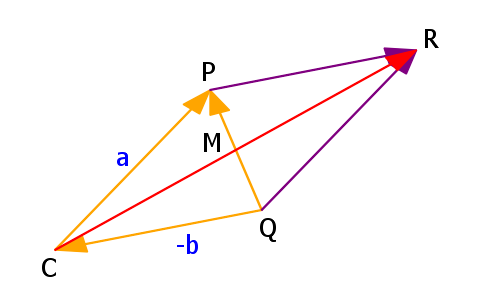
ベクトルCP=a、CQ=bと表すと残りの矢印(ベクトル)もみなaとbで表すことができる。
CPを平行移動したベクトルQR=a
CQを平行移動したPR=b
aもbも位置はどこでも構わない。
大きさ(長さ)と向きが同じならば同じベクトル。
上の図のCQの矢印の向きはQからCになっているが、QC=-b
a+b=CR。平行四辺形CPRQの対角線。
a-b=QP。平行四辺形CPRQのもう1つの対角線であり、三角形(△)CPQのもう1つの辺。
b-a=PQ。a-bと同じ大きさ。
PQ=CQ-CPといった具合にパッと書き換えられるようにしておく。
(a+b)/2=CM。CRの中点。
PQの中点も
CQ+(1/2)QP=b+(a-b)/2=(a+b)/2
2辺CP、CQの大きさ(長さ)が分かっていても△CPQの形・大きさは決まらないが、
2辺CP、CQの大きさと向きが決まっていれば、△CPQの形・大きさが1つに決まる。
つまり(平行でない)2つのベクトルa、bだけで三角形(△)が決まる。
a、bを数値で表記する場合、成分表示(言わば座標表示)になる。
たとえば、a=(3,4)、b=(4,1)といった具合。
( )の中の成分を縦に並べて書くこともできる。
ともかく(平面の場合)2つの数値があれば大きさと向きが決まり、もう1組あれば三角形(△)が決まる。
a、bの大きさ(すなわちスカラー)a、bは、それぞれ5、√17だが、ページの最後でもう一度触れる。
幸いベクトルの計算は、足し算・引き算難しくない。
たとえば、上の△CPQの頂点C、P、Qの座標をC (1,1)、P (4,5)、Q (5,2)とすると
x成分、y成分の引き算、足し算で、
a=(3,4)、b=(4,1)
b-a=(1, -3)、a-b=(-1,3)
a+b=(7,5)
※ 点Rの座標は始点Cの座標 (1,1)を足して(8,6)
(a+b)/2=(7/2,5/2)
※ 点Mの座標は(1,1)を足して(9/2,7/2)
となる。
a、bはx方向、y方向の単位ベクトル(大きさ1のベクトル)i、jを使って、
a=3i+4j、b=4i+jと表記することもできる。
i=(1,0)、j=(0,1)なので、
a=3・(1,0)+4・(0,1)=(3,4)
b=4・(1,0)+1・(0,1)=(4,1)
といった具合。
位置ベクトル
下の図の△CPQと△OABは同じ形・大きさの三角形。合同。位置が違うだけ。
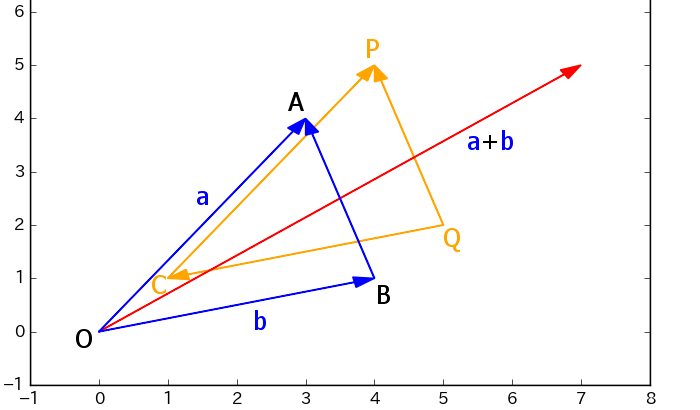
a、bと同じベクトルは無数に存在しうるが、
X-Y座標の原点O (0,0)を始点としたa、bは、その終点が座標そのものになる。
a=OA、b=OB
一番分かりやすい位置のベクトル。
OC=(1,1)、OP=(4,5)、OQ=(5,2)も
点C、P、Qの座標そのもの。
上の図の△OABを点Cの座標分つまりx方向に1、y方向に1移動させると△CPQと重なる。
OA=CP=a
OB=CQ=b
CP=OP-OC=(3,4)=a
CQ=OQ-OC=(4,1)=b
点A、Bの座標。
△CPQも△OABもベクトル的には同じ。a、bは同じ。
なお、OC-OC=CC=o(零ベクトル)。
ABの中点もPQの中点も (a+b)/2=(7/2,5/2)
ただし、ABの中点の座標は、(OA+OB)/2=(7/2,5/2)
PQの中点(点M)の座標は、(OP+OQ)/2=(9/2,7/2)
内分・外分、
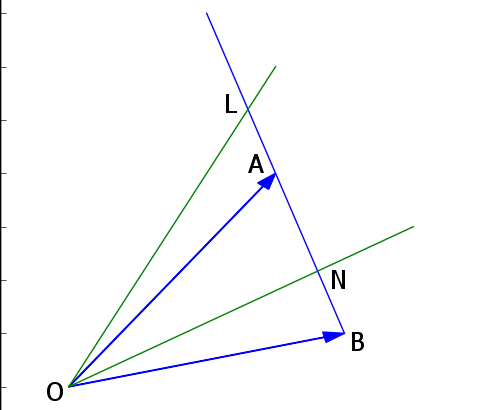
線分の中点は線分が1:1に分けられる点(等しく内分される点)だが、
線分ABがm:nに分けられる場合、
つまりBN=n、NA=mのとき、
内分点Nの位置ベクトル ON=(na+mb)/(m+n)
たすきがけのイメージ。
m=n=1のとき、(a+b)/2になる。
外分も分け方を覚えておく。
前回のメネラウスの定理や方冪(べき)の定理も覚えやすくなる。
行って戻ってのイメージ。
線分BAをn:mに外分する点をLとしたとき、
つまりBL=n、LA=mのとき、
外分点Lの位置ベクトル OL=(na-mb)/(-m+n)
線分ABをm:nに外分する場合は、(-na+mb)/(m-n)
三角形の重心
三角形の重心は頂点から重心を通る中線を2:1に内分する点。
△CPQの重心 Gは一番上の図1において
CG=(2/3) CM
CM=(a+b)/2なので、
CG=(a+b)/3
Gは線分CMを2:1に内分する点なので、上の内分点の位置ベクトルの式に当てはめてみると
OG=(OC+2OM)/3
OM=(OP+OQ)/2なので、
OG=(OC+OP+OQ)/3=(10/3,8/3)
△OABの重心は、(OO+OA+OB)/3=(a+b)/3=(7/3,5/3)
OG=OC+CGでもある。
一般に△ABCの位置ベクトルがa、b、cならば、重心の位置ベクトルは、
(a+b+c)/3。
ベクトルの大きさ
いつまで経ってもベクトルとベクトルの割り算が出てこない---
となれば、難しくない---
と思ったこともあるが、
掛け算がa・bとa×bで違う。
a・b=b・aなのにa×b=b×aではない。
ホワイですね。
とりあえず最初は2次元(平面)なので、a・bだけ。
この場合のベクトルとベクトルの積はベクトルにならずスカラー。
積は積でも内積(スカラー積)と呼ばれ、
x成分同士、y成分同士掛けたものを足し合わせると得られる。
a=(s,t)、b=(u,v)のとき、a・b=s・u+t・v
a=(3,4)、b=(4,1)ならば、a・b=16
a・a、b・b は、それぞれa、b の大きさの2乗。つまり
|a|=a=√(s2+t2)、|b|=b=√(u2+v2) ・・・ ルートです
a=5、b=√17
となる。
このへんで一区切り。
直線や円は、従来の方程式つまりy=ax+bやx2+y2=r2などでシンプルに表せるが、
三角形、四角形、多角形の方程式はシンプルとは言い難く、見掛けることもほとんどない。
そんな時にベクトル現る。
ベクトルを使うと分点など割り出せて、三角形の重心も容易に求まる。
直線も円もベクトルで表せるので(ベクトル方程式)、
ベクトルを使った表現方法も学んでおくと、あとあといろいろ理解できるようになる……。