前回に続いて等加速度の運動。今回は斜め下、斜め上。
滑らかな斜面上の運動
直線運動は水平方向、鉛直方向の他、斜面上の運動もある。
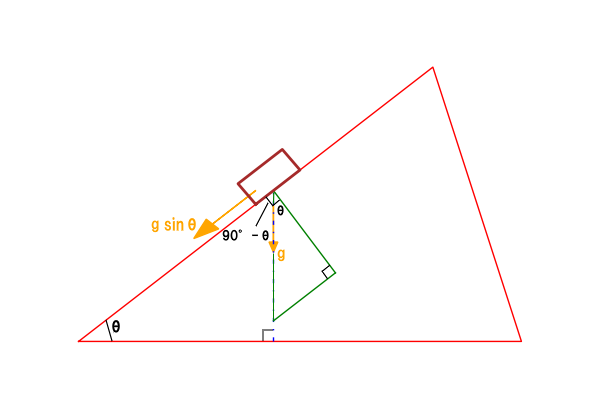
床との摩擦がない場合(滑らかな場合)、斜角 θの斜面を初速 v0で滑り降りる物体(ここでは質点)の斜面方向の加速度 a(斜め下を+)は、
ma = mg sinθ
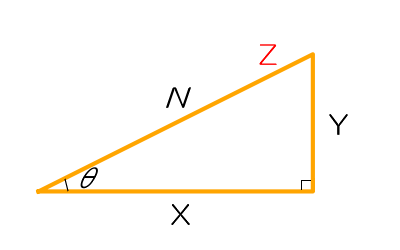
※ 垂線=斜辺×sinθ
運動方程式だが、mが消えて、
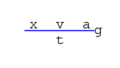
dv/dt = g sinθ
⇒ v = g sinθ t + v0
これはv = at + v0のaにg sinθを入れた式
さらにdx/dt = g sinθ t + v0なので、
⇒ Δx = (1/2) g sinθ t2 + v0t
これはΔx = x - x0 = (1/2)at2 + v0tのaにg sinθを入れた式
θ=0°のとき、水平方向の等速[度]直線運動
sin 0=0なので、
v = v0
Δx = v0t
θ=90°のとき、鉛直方向の自由落下と同じ。
sin 90=1、y方向の下が+なので、
v = gt + v0
Δy = (1/2)gt2 + v0t
滑らかでない斜面、床では摩擦係数がかかる。
運動方程式はまた別の機会に。
放物線運動
鉛直方向ではない落下、投げ上げ運動。斜め下、斜め上。
斜角 θ、初速 v0で斜め上に投げ上げられた物体(質点)は、
水平方向と鉛直方向に分けられて、
水平方向は等速[度]直線運動、
鉛直方向は等加速度(重力加速度) gの投げ上げ・自由落下。
v0の水平成分 v0 cosθ
※ 底辺=斜辺×cosθ
v0の鉛直成分 v0 sinθ
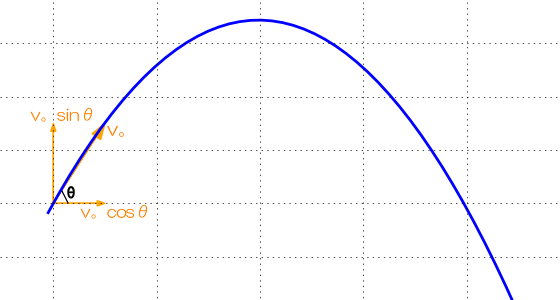
vx = v0 cosθ
Δx = v0 cosθ・t
vy = -gt + v0 sinθ
Δy = -(1/2)gt2 + v0 sinθ・t
x-y 放物線軌道
時間 tを消去するとx-yの式になる。
t = Δx/(v0 cosθ)をΔyの式に代入。
Δy = -(1/2)g(Δx/v0 cosθ)2 + v0 sinθ・(Δx/v0 cosθ)
Δy = -gΔx2/(2v02cos2θ) + tanθ・Δx
y = Ax2 + Bxの形
yの最大値 ymaxは、
y’ = 2Ax + B = 0のとき ・・・ 微分
⇒ x = -B/2Aのとき
⇒ x = tanθ / {g/(v02cos2θ)} = (v02sinθcosθ)/gのとき
※ tanθ=sinθ/cosθ
ymax = -(v02sin2θ)/2g + (v02sin2θ)/g = (v02sin2θ)/2g
t = (v0sinθ)/g
vy=0のとき最高点 ymaxなので、
tを求めてからx、ymaxを求めたほうが簡単。
なお、投げ下げた場合、vy > v0 > 0。放物線軌道の最高点はt < 0側(下図の黄色)。
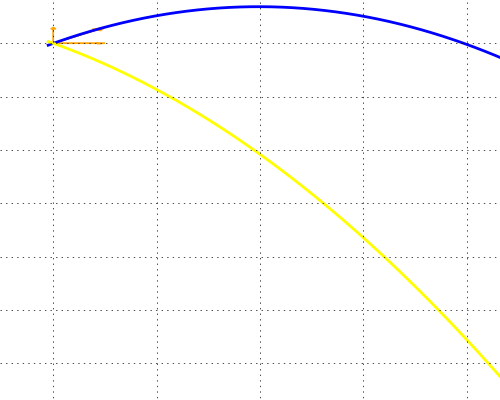
t≠0、Δy=0のとき、元の高さに落下
Δx = (2v02sinθcosθ)/g
t = (2v0sinθ)/g
地上から斜角30°で打ち上がったボールが120m先、地上高さ10mのところに飛んでいきました---
---放物線軌道の式(空気抵抗無視) Δy = -gΔx2/(2v02cos2θ) + tanθ・Δxに値を代入
10 = -9.8・1202 /(2v02・3/4) + (1/√3)・120
v0 = 39.8[m/s] = 143.4[km/h]
軌道要素 (x、y)、v、θ、tを与えて、求めて、……
ポイント --- sin・cos・tanに惑わされない。
追)sin・cos・tanおよびsinθcosθの最大について
曲線運動は他にも
円運動
楕円運動
双曲線運動
などがある。